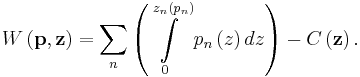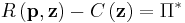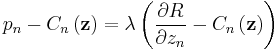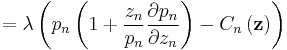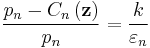Ramsey problem
The Ramsey problem, or Ramsey-Boiteux pricing, is a policy rule concerning what price a monopolist should set, in order to maximize social welfare, subject to a constraint on profit. A closely related problem arises in relation to optimal taxation of commodities.
For any monopoly, the price markup should be inverse to the price elasticity of demand: the more elastic demand for the product, the smaller the price markup. This was stated by J. Robinson (1933) but it has been recognized later that Frank Ramsey has found the result before (1927) in another context (taxation). The rule was later applied by Marcel Boiteux (1956) to natural monopolies (decreasing mean cost): a natural monopoly experiences profit losses if it is forced to fix its output price at the marginal cost. Hence the Ramsey-Boiteux pricing consists into maximizing the total welfare under the condition of non-negative profit, that is, zero profit. In the Ramsey-Boiteux pricing, the markup of each commodity is also inversely proportional to the elasticities of demand but it is smaller as the inverse elasticity of demand is multiplied by a constant lower than 1.
It is applicable to public utilities or regulation of natural monopolies, such as telecom firms.
Ramsey pricing is sometimes consistent with a government’s objectives because Ramsey pricing is economically efficient in the sense that it can maximize welfare under certain circumstances. There are, however, problems with Ramsey pricing. A profit-maximizing operator will choose Ramsey prices only if all markets are equally monopolistic or equally competitive. If markets are not equally monopolistic or competitive, then the regulator has an interest in ensuring that the extent to which the operator can use Ramsey pricing is limited to groups of services that are subject to similar degrees of competition. Regulators typically do this by forming groups of services that are subject to similar degrees of competition and allowing the operator price flexibility within each service group. Even though Ramsey pricing can be economically efficient, it may not be consistent with the government’s goal of providing affordable service to the poor and the rate by which prices change to achieve Ramsey-efficient prices may not be consistent with political sustainability. As a result of these two concerns, the regulator sometimes limits the operator’s ability to pursue Ramsey pricing within a service group. In the case of services to the poor, the regulator may place upper limits on the prices. In the case of services where traditional prices were different from Ramsey prices, there are equity issues in changing from the traditional pricing structure to a new structure, even if the new structure would be more efficient in an aggregate sense. In such situations, the regulator may impose pricing restrictions that prevent Ramsey pricing or that impose a slower transition to Ramsey pricing than the operator would choose left to its own devices.
Lastly, regulators often note that Ramsey pricing is a form of price discrimination—although not necessarily a bad form of price discrimination—and customers sometimes object to it on that basis. The public sometimes believes that it is unfair to cause one type of customer to pay a greater mark-up above marginal cost than another type of customer. In such situations regulators may further limit an operator’s ability to adopt Ramsey prices. [1]
Practical issues exist with attempts to use Ramsey pricing for setting utility prices. It may be difficult to obtain data on different price elasticities for different customer groups. Also, some customers with relatively inelastic demands may acquire a strong incentive to seek alternatives if charged higher markups, thus undermining the method. Politically, customers with relatively inelastic demands may also be considered as those for whom the service is more necessary or vital; charging them greater markups can be challenged as unfair.
Formal presentation and solution
Consider the problem of a regulator seeking to set prices 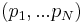 for a multi-product monopolist with costs
for a multi-product monopolist with costs 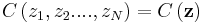 where
where 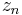 is the output of good n and
is the output of good n and 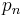 is the price. Suppose that the products are sold in separate markets (this is commonly the case) so demands are independent, and demand for good n is
is the price. Suppose that the products are sold in separate markets (this is commonly the case) so demands are independent, and demand for good n is 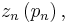 with inverse demand function
with inverse demand function 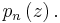 Total revenue is
Total revenue is 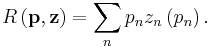
Total surplus is given by
The problem is to maximize 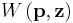 subject to the requirement that profit
subject to the requirement that profit 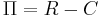 should be equal to some fixed value
should be equal to some fixed value 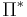 . Typically, the fixed value is zero to guarantee that the profit losses are eliminated.
. Typically, the fixed value is zero to guarantee that the profit losses are eliminated.
This problem may be solved using the Lagrange multiplier technique to yield the optimal output values, and backing out the optimal prices. The first order conditions on 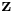 are
are
where  is a Lagrange multiplier and Cn(z) is the partial derivative of C(z) with respect to zn, evaluated at z.
is a Lagrange multiplier and Cn(z) is the partial derivative of C(z) with respect to zn, evaluated at z.
Dividing by 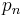 and rearranging yields
and rearranging yields
where 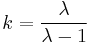 is lower than 1 and
is lower than 1 and 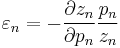 is the elasticity of demand for good
is the elasticity of demand for good 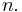 That is, the price markup over marginal cost for good
That is, the price markup over marginal cost for good  is again inversely proportional to the elasticity of demand but it is smaller. The monopoly is in a second-best equilibrium, between ordinary monopoly and perfect competition.
is again inversely proportional to the elasticity of demand but it is smaller. The monopoly is in a second-best equilibrium, between ordinary monopoly and perfect competition.
Ramsey condition
An easier way to solve this problem in a two-output context is the Ramsey condition. According to Ramsey, as to minimize deadweight losses, one must increase prices to rigid and elastic demands in the same proportion, in relation to the prices that would be charged at the first-best solution (price equal to marginal cost).
References
- ^ Body of Knowledge on Infrastructure Regulation “Tariff Design: Economics of Tariff Design – Deviations from Marginal Cost Pricing: Ramsey Pricing”